1) En el circuito que se muestra en la figura C1=5μf ,C2=15μf, C3=3μf y △VF=24V

Calcular:

a)Calcular la carga en cada capacitor

b)La diferencia de potencial en cada capacitor

c)La energía almacenada en cada capacitor

d)La energía total del sistema

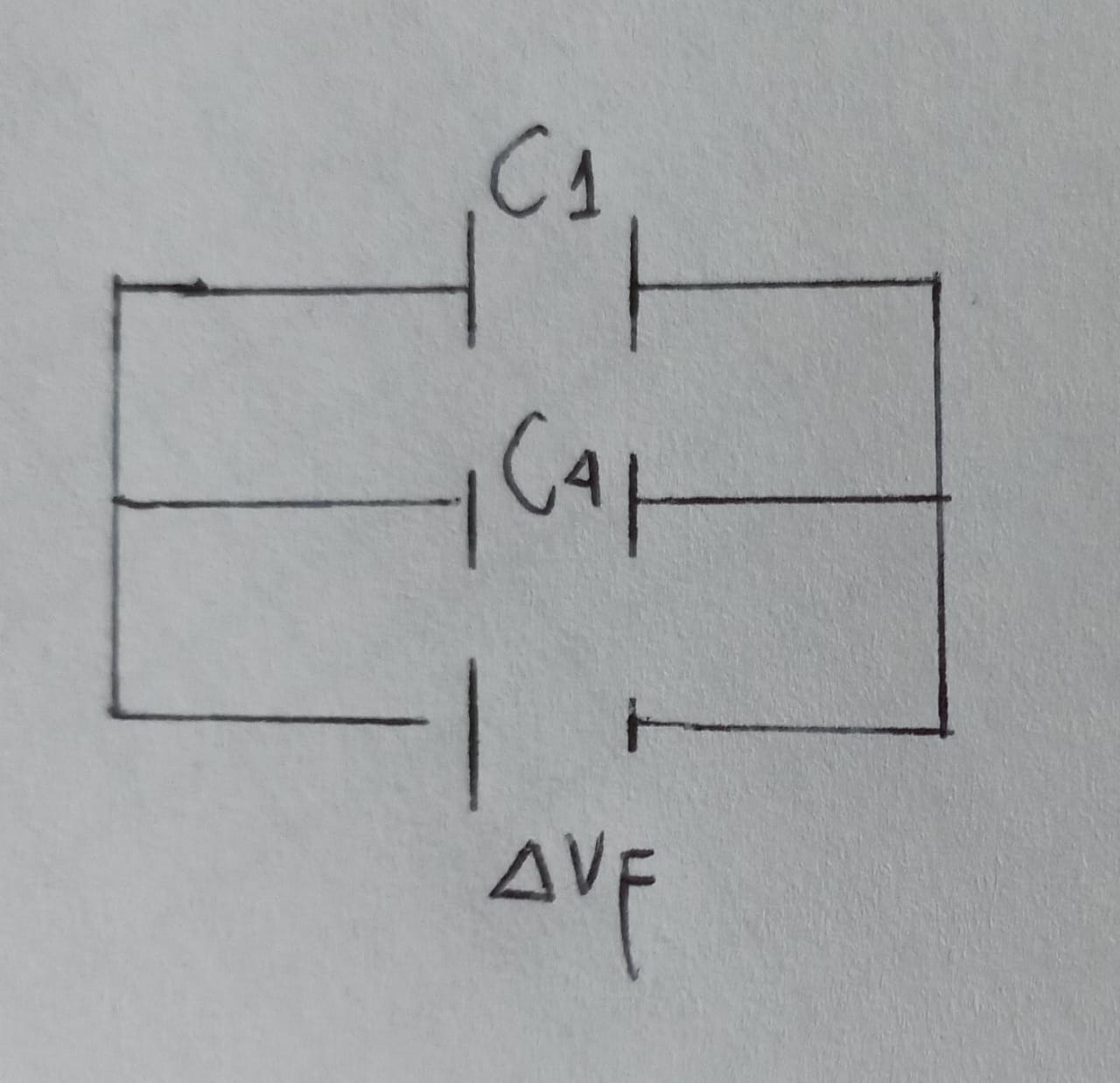
Cómo C1 tiene △V=24v

entonces Q 1=△V*C1

Q1=24V*5μf

Q1=120μc

entonces Q4=△V*C1

Q1=24V*10μf

Q1=240μc

como Q4 es el resultado de dos capacitores en serie que tienen la misma carga

Q2=Q3=240μc

La diferencia de potencial △V=Q/C

Entonces △V1=120μc/5μf

△V1=24V

△V2=250μc/15μf

△V2=16V

△V3=240μc/30μf

△V3=8V

Energía en cada capacitor y la energía total

½ Q^2/C

U1=½*(120x10^-6)^2/5X10^-6

U1=1.44x10^-3J

U2=½*(240x10^-6)^2/15X10^-6

2=1.92x10^-3J

U3=½*(240x10^-6)^2/30X10^-6

U3=9.6x10^-4J

Energía total

Ut=U1+U2+U3

Ut=1.44x10^-3J+1.92x10^-3J+9.6x10^-4J

Ut=4.32x10^-3J

2)

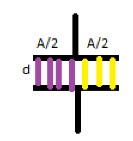
K1=Morado

K2=Amarillo

Hallar C para cada arreglo

   a)Se toma como dos capacitores en paralelo

c=c1+c2

Como Co=AE0/d -> C=kCo

Para K1=C1=A/2E0/d

C1=E0K1A/2d

Para K2=C2=A/2E0/d

C2=E0K2A/2d

C=E0K1A/2d+E0K2A/2d

C=E0K1A+E0K2A

C=E0/A (K1+K2)

b) (1/c1+1/c2)-1

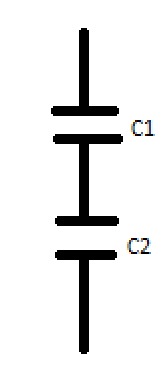
C1=AE0/d

C1=K1AE0/d/2 =C1=2K1AE0/d

C2=K2AE0/d/2 =C2=2K2AE0/d

C=(d/2K1AE0+d/2K2AE0)-1

C=(K2d+K1d/2E0AK1K2)-1

C=2EOAK1K2/K2d+K1d

C=2EoA/d(K1K2/k1+K2)

3) Un capacitor está constituido por dos cilindros coaxiales de hierro, huecos un dentro del otro, la carga del capacitor es 10pc, el cilindro interior tiene radio de 0,5 mm y el exterior de 5 mm. La longitud del cilindro es de 18cm. Calcule la capacitancia y la diferencia de potencial.

primero tendremos en cuenta los datos que nos dan en el enunciado

Q=10PC

a=0.5mm

b=5mm

l=18cm

Hallar

a)capacitancia

c=2πE0l/ln(a/b)

c=2π(8.85x10^-12)(0,18)/ln(5x10^-3/0,5x10^-3)

c=4,35x10^-12 f

c=4,35 pf

b)△v=Q/2πE0l*ln(b/a)

△v=10x10^-12/2π(8.85x10^-12)(0,18)*ln(5x10^-3/0,5x10^-3)

△v=2,3V